Simplifying Radicals: A Comprehensive Guide To Finding The Simplest Radical Form
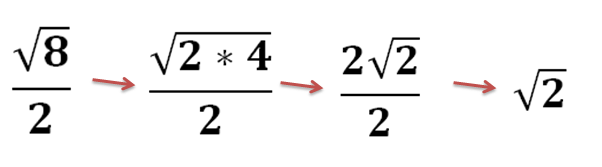
Simplifying Radicals: A Comprehensive Guide To Finding The Simplest Radical Form. Discover more detailed and exciting information on our website. Click the link below to start your adventure: Visit Best Website. Don't miss out!
Table of Contents
Simplifying Radicals: A Comprehensive Guide to Finding the Simplest Radical Form
Simplifying radicals might sound intimidating, but mastering this fundamental algebra skill unlocks a deeper understanding of mathematics and significantly improves problem-solving abilities. This comprehensive guide provides a step-by-step approach to simplifying radicals, ensuring you can confidently tackle even the most complex expressions. Whether you're a high school student prepping for exams or an adult learner brushing up on your math skills, this guide is your key to understanding radical simplification.
What are Radicals?
Before diving into simplification, let's clarify what radicals are. In mathematics, a radical expression is one that contains a radical symbol (√), indicating a root (like a square root, cube root, etc.) of a number. For example, √25, ∛8, and ⁴√16 are all radical expressions. The number inside the radical symbol is called the radicand. The small number outside the radical symbol (2 for square root, 3 for cube root, etc.) is called the index. If no index is written, it's understood to be 2 (a square root).
Why Simplify Radicals?
Simplifying radicals is crucial because it allows you to express mathematical expressions in their most concise and manageable form. Unsimplified radicals can make calculations more complicated and obscure underlying mathematical relationships. Simplifying them enhances clarity and efficiency in various mathematical contexts.
Step-by-Step Guide to Simplifying Radicals
Simplifying radicals involves breaking down the radicand into its prime factors and then extracting any perfect roots. Here's a step-by-step process:
1. Prime Factorization:
- Begin by finding the prime factorization of the radicand. This means expressing the number as a product of its prime factors (numbers divisible only by 1 and themselves). For example, the prime factorization of 72 is 2 x 2 x 2 x 3 x 3 = 2³ x 3².
2. Identifying Perfect Roots:
- Once you have the prime factorization, identify any factors that are perfect squares, perfect cubes, or perfect nth powers, depending on the index of the radical.
- For a square root (index = 2), look for pairs of identical prime factors.
- For a cube root (index = 3), look for triplets of identical prime factors.
- For a fourth root (index = 4), look for quadruplets of identical prime factors, and so on.
3. Extracting Perfect Roots:
- For each set of perfect nth powers, extract the root. For example:
- √(2² x 3²) = √2² x √3² = 2 x 3 = 6
- ∛(2³ x 3³) = ∛2³ x ∛3³ = 2 x 3 = 6
- ⁴√(2⁴ x 3⁴) = ⁴√2⁴ x ⁴√3⁴ = 2 x 3 = 6
4. Combining Remaining Factors:
- Any prime factors that do not form a perfect nth power remain under the radical sign. Multiply these remaining factors together.
Example: Simplifying √72
- Prime Factorization: 72 = 2 x 2 x 2 x 3 x 3 = 2³ x 3²
- Identifying Perfect Squares: We have one pair of 2s (2²) and one pair of 3s (3²).
- Extracting Perfect Squares: √2² = 2 and √3² = 3
- Combining Remaining Factors: √72 simplifies to 2 x 3√2 = 6√2
Simplifying Radicals with Variables
The process for simplifying radicals with variables is similar. Remember the rules of exponents:
- √x² = |x| (absolute value is crucial for even roots)
- ∛x³ = x
- ⁴√x⁴ = |x| (absolute value is crucial for even roots)
Advanced Techniques and Practice
For more advanced techniques, explore simplifying radicals with fractions and dealing with nested radicals. Practice is key to mastering radical simplification. Numerous online resources, including practice problems and worksheets, are readily available to help you hone your skills.
Conclusion
Mastering radical simplification is a significant step towards improving your overall mathematical proficiency. By following the steps outlined in this guide and practicing regularly, you can confidently simplify even the most complex radical expressions. Start practicing today and unlock a deeper understanding of the world of mathematics!
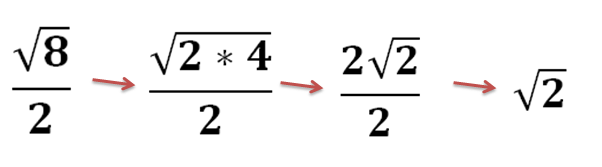
Thank you for visiting our website wich cover about Simplifying Radicals: A Comprehensive Guide To Finding The Simplest Radical Form. We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and dont miss to bookmark.
Featured Posts
-
 What Happens 12 Weeks From Today A Date Calculator And Guide
Feb 05, 2025
What Happens 12 Weeks From Today A Date Calculator And Guide
Feb 05, 2025 -
 Peaches Unexpected Journey A Logging Camp Adventure
Feb 05, 2025
Peaches Unexpected Journey A Logging Camp Adventure
Feb 05, 2025 -
 Encore Des Pannes Sur La Ligne Rem Voici Ce Que Vous Devez Savoir
Feb 05, 2025
Encore Des Pannes Sur La Ligne Rem Voici Ce Que Vous Devez Savoir
Feb 05, 2025 -
 All The Fallen A Global Look At Memorials And Commemorations
Feb 05, 2025
All The Fallen A Global Look At Memorials And Commemorations
Feb 05, 2025 -
 Afl World In Shock Remembering Troy Selwood 40
Feb 05, 2025
Afl World In Shock Remembering Troy Selwood 40
Feb 05, 2025
Latest Posts
-
 Survival Evasion Planning Preparing For Unexpected Challenges
Feb 05, 2025
Survival Evasion Planning Preparing For Unexpected Challenges
Feb 05, 2025 -
 Is A Buffy The Vampire Slayer Reboot Even Needed
Feb 05, 2025
Is A Buffy The Vampire Slayer Reboot Even Needed
Feb 05, 2025 -
 Is Caillou Sick Understanding His Portrayal In The Show
Feb 05, 2025
Is Caillou Sick Understanding His Portrayal In The Show
Feb 05, 2025 -
 World Cancer Day 2025 The Latest On Urologic Cancers
Feb 05, 2025
World Cancer Day 2025 The Latest On Urologic Cancers
Feb 05, 2025 -
 Comparativa De Brocas Ncm Para Concreto Cual Elegir
Feb 05, 2025
Comparativa De Brocas Ncm Para Concreto Cual Elegir
Feb 05, 2025
